The Problem with the Linda Problem

This article has been adapted from the book Psychonomics: The Scientific Conquest of the Mind.

The Tversky and Kahneman thought experiment known as the Linda Problem is one of the most popular and damning of its kind. Popular because you can’t read a book on behavioral economics or rational thinking without coming across it. Damning because, as everyone knows, it proves that we are all irrational. 

But, like most Behavioral Economics work, the experiment is founded on a basic fallacy that, if anything, proves that the researchers are the ones that are irrational. Here’s why.

Representativeness

One of the great biases known to psychology is a cognitive error called ‘Representativeness’ or ‘the Representativeness Heuristic’. The idea is that, in the process of estimating or predicting the probability of something, people tend to put too much emphasis on the familiarity or resemblance of the causes. If something is more familiar, they think it will be more probable. When asked to guess a student’s major, for instance, one will look at his characteristics, the way he acts and dresses, and so on, and make the estimation based on that representation. If he dresses slovenly and has pink hair, he is likely to be an art major; if he is clean-cut and formal, he is likely to be a business major, and so on.

While this seems fairly sensible, researchers have found that this kind of judgment goes on even when the probability of such an outcome is notably low. That is, one will say that the likelihood that the pink hair guy is an art major is high even if there is a very low percentage of art majors at the school. As researchers have found, people tend to put too great an emphasis on representation and less on other relevant facts that should serve as a baseline indicator. If only 3 percent of the students are art majors, the baseline for determining whether pink is an art student is 3 percent. Other factors will move the likelihood up or down, but the likelihood will still be around 3 percent. 

Thus, when people look at his pink hair and say that there is a high percentage chance (say, 70 or 80 percent) that he is an art student, they are allowing the Representativeness Bias to sway their estimates. They are being irrational, or so say behavioral economists.

Taking another look at it reveals that it isn’t so cut-and-dry. The fact is that we have good reasons for estimating what we estimate, and often take more into account than is realized. For instance, when judging the likelihood that a student with pink hair is an art major, one will probably consider all of the instances where he has encountered similar colored hair. When he cross references all of that information with the others’ majors, he will come up with an alternative baseline, one that might be better at identifying likelihood than the percentage of students who are art majors. One might have come across hundreds of students with pink hair and found them all to be art majors. In this case, the new baseline is around 100 percent no matter how uncommon art majors are at a particular school.

In this and other examples, past experience is invaluable in advancing judgment. Of course, if there are absolutely no art students at the school, then it would be irrational to think the pink-haired guy was an art major. But, as long as there is a chance, as long as there are some art students at the school, past experience should be applied in determining the likelihood.

The Linda Problem

One famous example by Tversky and Kahneman illustrates this puzzle well. In the experiment, Tversky and Kahneman introduce a woman, Linda, with the following description:

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

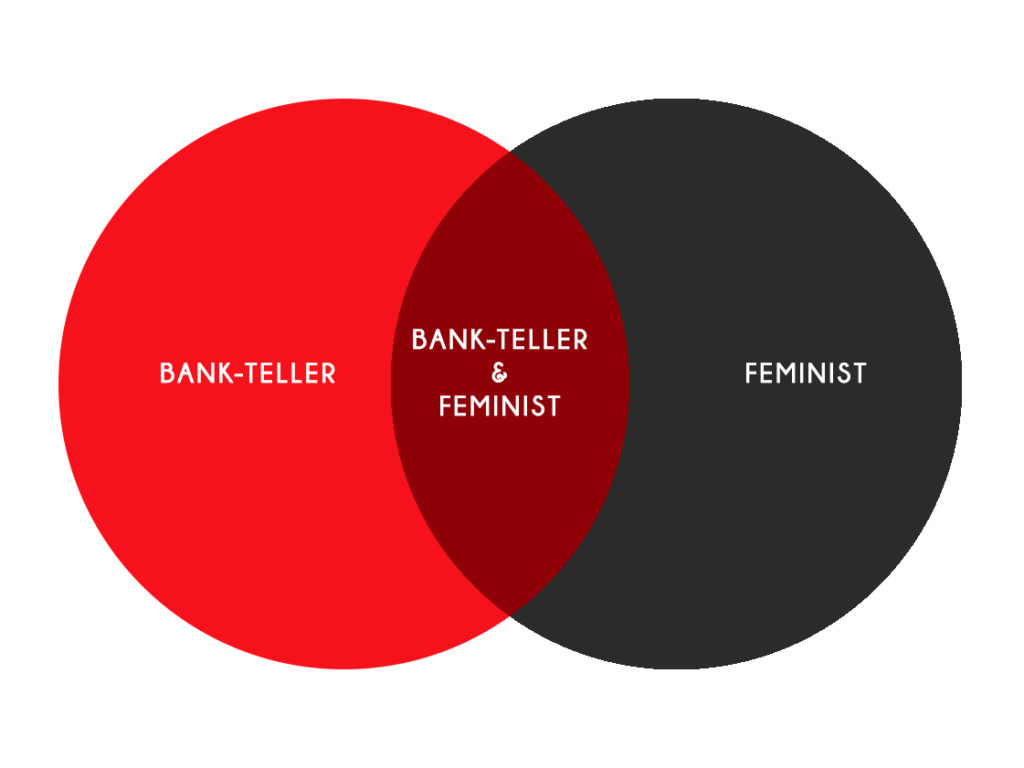
They then asked which is more probable, ‘(1) Linda is a bank teller’, or ‘(2) Linda is a bank teller and is active in the feminist movement’?

The answer that almost all people give is ‘(2) Linda is a bank teller and is active in the feminist movement’. Quite sensibly, it seems, anyone taking this test will read the information about Linda and surmise that she is definitely the kind of woman who would be active in the feminist movement, and so, seeing that the second option includes this little tidbit, chooses it over the other.

What is interesting about this experiment is that the vast majority of the subjects choose the second option as being more probable even though it includes two specific characteristics (that Linda is a bank teller and that she is active in the feminist movement) whereas the first has only one specific characteristic (that Linda is a bank teller). Technically speaking, no two characteristics are ever more probable than any of them on their own. It is always more probable for one to be tall than to be tall and good looking; to have freckles than to have freckles and be a concert pianist; and to be a U.S. citizen than to be both U.S. and Canadian citizen. X is always more probable than XY by virtue of mere mathematics.

And yet, it seems that the probability of the two happening together is higher. It just seems as though Linda is both bank teller and active in the feminist movement, so we claim that it is more probable. As such, researchers have identified a place where people consistently and predictably make incorrect estimates. They may well know that it is statistically impossible for two conditions to be more likely than one, but they still choose the two. Biologist Stephen J. Gould marveled at the paradox: “I know that the [conjoint] statement is least probable, yet a little homunculus in my head continues to jump up and down, shouting at me—‘But she can’t just be a bank teller; read the description!’ ”

Tversky and Kahneman explain this tendency, naturally, as a cognitive error. A kind of Representativeness Bias, the Linda phenomenon shows what Tversky and Kahneman call a ‘Conjunction Fallacy’, where one believes that specific conditions are more probable than single general ones. People think that the more specific conditions are, the more likely they are to match the represented reality, when, in fact, they become less and less statistically probable. 

So, what is going on here? And is it really as irrational as it seems? The reader might guess by now that there are good reasons for this tendency as there are for all the alleged cognitive errors. 

The Problem with Probability

First, it is necessary to take a different approach. In analyzing the Linda experiment, researchers have looked merely on the surface of the question asked—the statistical probability of either condition—and neglected the substance of each. In doing this, their answer is clear-cut and based in mathematics. Since the first answer has only one condition, it is more probable. End of story, right?

Wrong. Most test-takers do not do this. Instead, they look at the different options and choose which they believe is most representative of the personality described. Since Linda has all the traits of an active feminist, the option that includes anything having to do with feminism will be high on the list. In this example, only one option had anything having to do with feminism, so it was the obvious choice for the test-takers. The other option, bank teller, had nothing to do with Linda’s description—it would only be acceptable if there were something else in the option that redeemed it. As such, it is more likely that Linda is a bank teller and feminist because it includes the more accurate description of her character.

Of course, two conditions are always less statistically probable than either one by itself, and so it would seem that choosing the description with more characteristics is irrational even if it includes a more accurate description. But is this necessarily the best way to look at it? Certainly, test-takers do not look at it this way. They might envision a Venn diagram, and try to determine which sector Linda falls into. ‘Feminist’ has to be part of it, but plain old ‘feminist’ isn’t an option. ‘Bank teller’ is a bigger space, but it doesn’t include the relevant characteristic. So, it must be ‘bank teller and active in the feminist movement’. They don’t care that it contains two conditions whereas the first option contains only one. They are focused on the substance of the conditions.

And this makes more sense than one might assume. Indeed, as the question is framed, the test-taker will probably see the two conditions in the second and reconstruct the first so that it contains two characteristics. The thought process is something like this: ‘Since the second says that Linda is a bank teller and feminist, the first must really be saying that she is a bank teller and not a feminist.’ The way the question is framed makes such reconstruction inevitable—there is no logical reason why such uneven options would be given; if the second option considers feminism, then the first must do so passively by not mentioning it. In the end, both options have two conditions, one which includes feminism and one which does not.

Filling the Void

This principle of filling the void with a negative is integral to understanding how the mind works. Human beings assess the world around them by taking in sensory data and making a mental model of it. When a part of that pattern is left void, the mind fills it in with what it expects to be there. In lieu of a universal understanding of the world, we fill in gaps to make sense of what we do see. This is also why we see grayish dots at the intersections of crosshairs, and why we see the still deck of a ship move after staring out at the passing waves. We build a mental pattern of the way the world works, and, when a piece is missing, our minds fill it in with whatever is expected. In the case of the Linda experiment, the piece missing is the mention of ‘feminism’ in the first option. Since it isn’t there, we automatically fill it in with the expected piece—‘not active in the feminist movement’.

So, the two options are really seen as both having two parts, one about her profession and one about her involvement in the feminist movement. Since both have the same part about her profession (‘bank teller’), that part is canceled out. The fact that it’s in both parts means it’s not really asking about her profession—it’s only asking about feminism. The subject whittles the question down to this: ‘Which is more probable? That Linda is not in the feminist movement or that she is in the feminist movement.’ And, quite rationally, people choose the second.

And this will apply to as many spaces as the pattern suggests. If, for example, the options were not two, but seven, and followed a similar building pattern, the mind would automatically fill in the others as a matter of course.

• Bank teller
• Bank teller, golfer
• Bank teller, golfer, trapeze artist
• Bank teller, golfer, trapeze artist, avid reader
• Bank teller, golfer, trapeze artist, avid reader, pianist
• Bank teller, golfer, trapeze artist, avid reader, pianist, stamp collector
• Bank teller, golfer, trapeze artist, avid reader, pianist, stamp collector, active in the feminist movement

Now, it is obvious that the first is most statistically probable because it has the fewest conditions and is included in all the others. And, by the standard of behavioral economists, it would be irrational to choose any other option as more probable. But the logical test-taker cannot view the options as they are. In order to make sense of the question, he will reconstruct the options and include the missing pieces as negatives:

• Bank teller, not golfer, not trapeze artist, not avid reader, not pianist, not stamp collector, not active in the feminist movement
• Bank teller, golfer, not trapeze artist, not avid reader, not pianist, not stamp collector, not active in the feminist movement
• Bank teller, golfer, trapeze artist, not avid reader, not pianist, not stamp collector, not active in the feminist movement
• Bank teller, golfer, trapeze artist, avid reader, not pianist, not stamp collector, not active in the feminist movement
• Bank teller, golfer, trapeze artist, avid reader, pianist, not stamp collector, not active in the feminist movement
• Bank teller, golfer, trapeze artist, avid reader, pianist, stamp collector, not active in the feminist movement
• Bank teller, golfer, trapeze artist, avid reader, pianist, stamp collector, active in the feminist movement

As we can see, even though the seventh option is the only one in which all seven conditions were listed outright, each of the options has all the different conditions included, only as negatives. They are all equally conjoint and, as such, the only way we can judge the probability is if we look at the representativeness of the subject. We would do best to pick the one that included the most accurate description, which, in this example, is the last condition, ‘active in the feminist movement’, and which only option seven includes as a positive. 

On the surface, of course, this is preposterous. How could the last one be more likely than the first one when the last includes the first in it and a bunch of others? But with another perspective, the answer is clear. The first necessarily excludes the most important ingredient, and so must be rejected.

When taken at face value, experiments aimed at proving Representativeness are straightforward and plain. Of course the single condition is less probable than the conjoint condition, and it is obvious that anyone who thinks otherwise must be irrational. When we fall into the trap ourselves, like Gould, we rack our brains to explain the paradox. But, ultimately, there is no need. The paradox is an illusion engineered by the researchers, and the instinctive response is actually the correct one.

This article has been adapted from the book Psychonomics: The Scientific Conquest of the Mind.